Optimization Mathematics
Mathematics behind the scenes
So how exactly does mathematical optimization work? Mathematical optimization first tries to abstract given situations from the real world in the form of models. This step is also called modeling. The resulting model (also called problem), which is set up with the help of information from the application partners, can now be solved by means of algorithms. Special problem types can be approached problem-specifically with special algorithms in order to reduce the runtime.
Here we can see an example of a model:
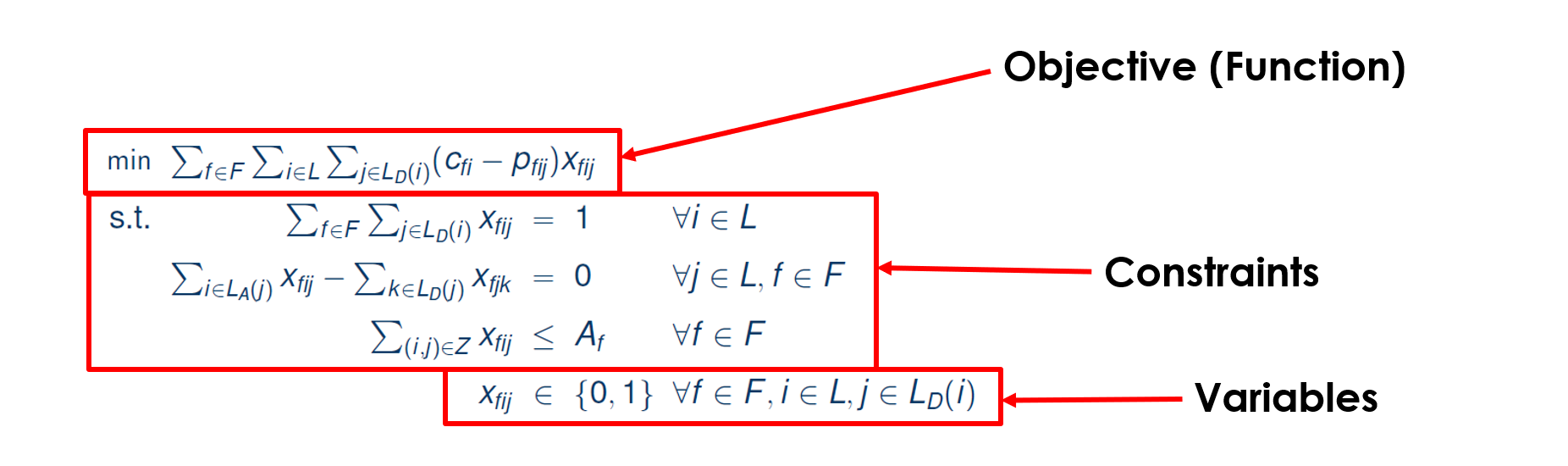
This consists of three different components:
- Objective
- Constraints
- Variables
We deal with the variables first, since they form the basis for change and adjustment in all other parts of our mathematical model. The variables are also crucial for the characterization of the problem.
Variables
Variables are placeholders and should be either directly controllable by the user or indirectly changeable by the context in constraint. It applies: At least a part of the variables of the problem should be controllable! One distinguishes variables on the basis of the values, which they may assume:
Binary Variables

Binary variables can only take two values, 0 and 1. These variables can map yes/no decisions: Should we produce or not? Do we exceed a critical limit or not? Do we want to switch on a machine or not?
Integer Variables

Integer variables can reflect a number of indivisible elements. For example, which car manufacturer wants to produce only half a car? Which ship repair company wants to produce only half a ship? Units that are only useful as a whole can be represented in this way.
Continuous Variables

Continuous variables can represent all machine-detectable numbers. In the context of computer science these would be the variable types float and double. These are interesting for all measured values which do not exclusively accept whole numbers: These include, for example, times, lengths and volumes.
Objective
The declared goal of the optimization process is represented in the mathematical sense by the objective function. In principle, there are two directions in which optimization can take place: Maximize versus Minimize. Examples are the following:
- MAXIMIZE profit, sales, customer satisfaction, safety
- MINIMIZE costs, risks, absences, delays, waste
Most often, one tries to find an adequate average of all target function aspects to be considered. Therefore, it is necessary to quantify all optimization dimensions in the form of a unit. This is mostly done by monetary units. In many cases, cost rates can be easily determined, such as a company's sales, which are accurately documented. However, expressing customer satisfaction in monetary units is rather difficult, as it is accompanied by many imponderables: Will the customer continue to buy his next product from the same company? / How damaging are unhappy customers in the form of reviews for the company?
Constraints
In order to be able to represent reality, technical and also abstract facts have to be modeled. This is done for the most part in constraints. Loosely speaking, constraints serve two purposes:
- Constraints can restrict variables with so-called bounds
- Constraints can create variable links and thus make them dependent on each other
For a better understanding, an example may be helpful. Let us assume two continuous variables x and y. Both can initially assume all values on the axis of the real numbers. Let us now imagine that x represents the number of goods produced and y, for example, the sales of the company. Let us further imagine that each good brings in 100€ for the company and that we have a maximum of resources to produce 1000 goods:
- Ressource-Constraint (bounds): x ≤ 1000
- Sales-Constraint (link): y = 1000*x
For the sake of completeness, it should be mentioned here that equations can be used and inequalities must always result in closed sets with ≤ and ≥, which means that < and > are not allowed in general. Why? Please name the smallest possible real number, which is really greater than zero...