Optimization LP-Solver App
Introduction
If you want to learn more about the LP-Solver app, you should first understand what constitutes a mathematical optimization problem and what a linear problem / program is. If you don't know that yet, please visit Application, Mathematics or Linear Problem Example. The LP-Solver app is designed for didactic purposes and to introduce the concept and possibilities of mathematical optimization to pupils, students or industry partners. The app can be used to create your own models, to demonstrate randomized models or even to interpret larger files in LP format as a model. All these models can of course be solved afterwards. It should be noted that this app may not be used for commercial purposes, as no guarantee is given for the solutions. In addition, the app is not designed for solving large models. For this, fall back on solver alternatives in the area of programming on a computer.
Model LP yourself
The LP solver can be used to enter your own models. For this the model can be entered user-friendly without being restricted by syntax. To make the input as simple as possible, an own keyboard was implemented, which contains the most important necessary character sets. Thus, any number of constraints can be entered and added. In case of typing errors, these can also be removed and added again. If syntactical errors occur, you will be informed in a message and can easily correct the input. Afterwards, the entered model can be viewed completely and then solved.

1. Select the upper Button "Build new model"
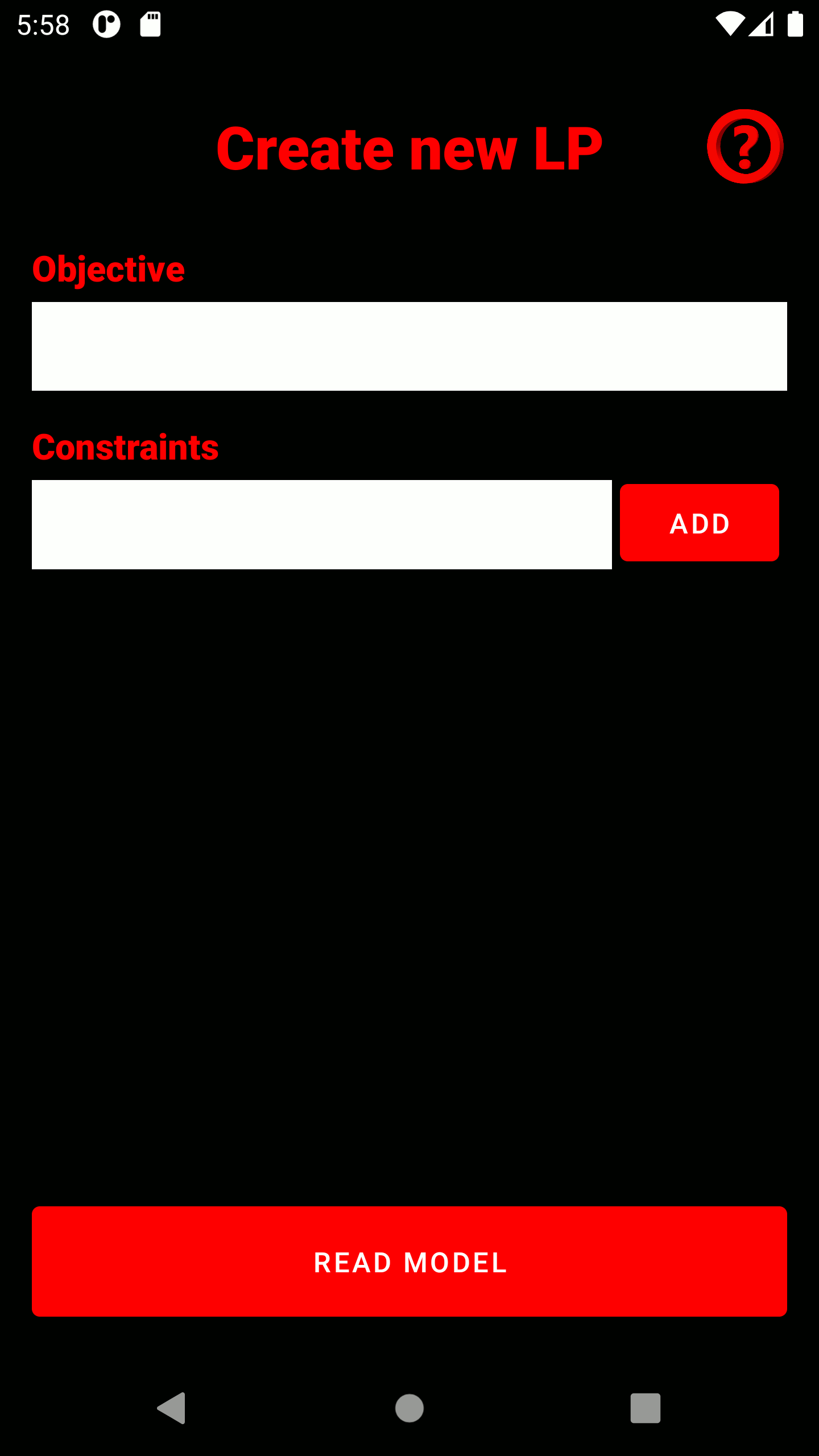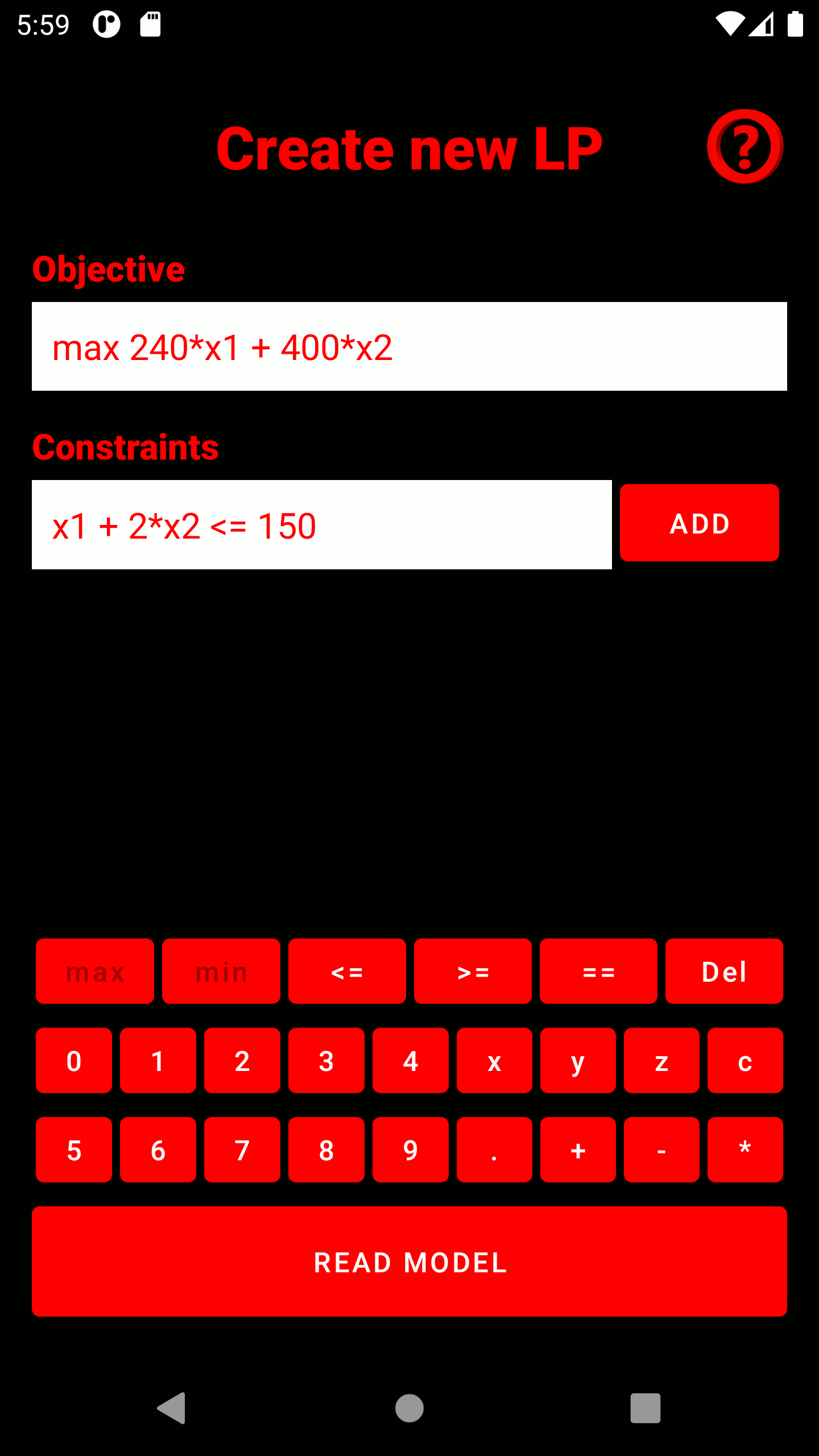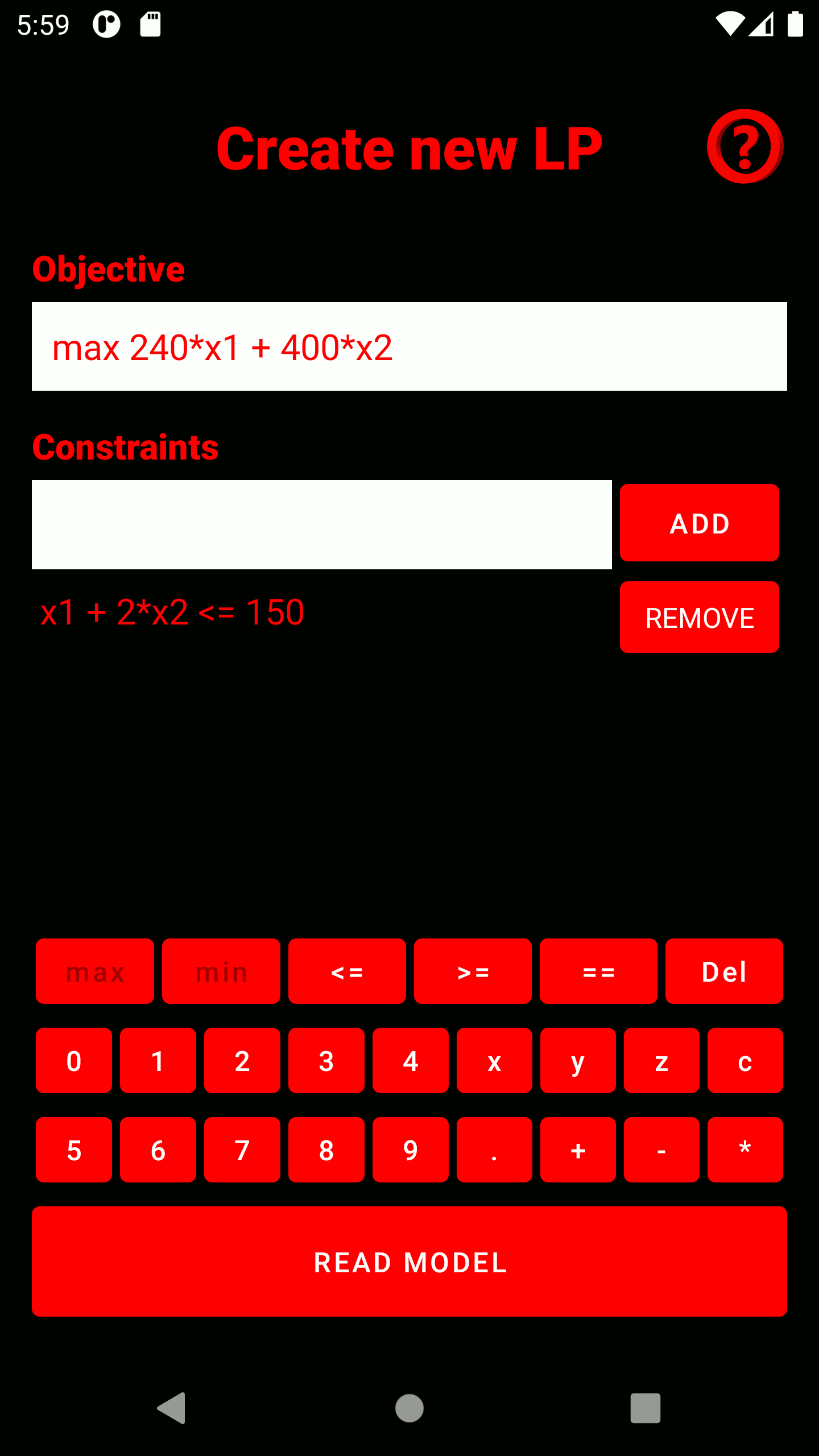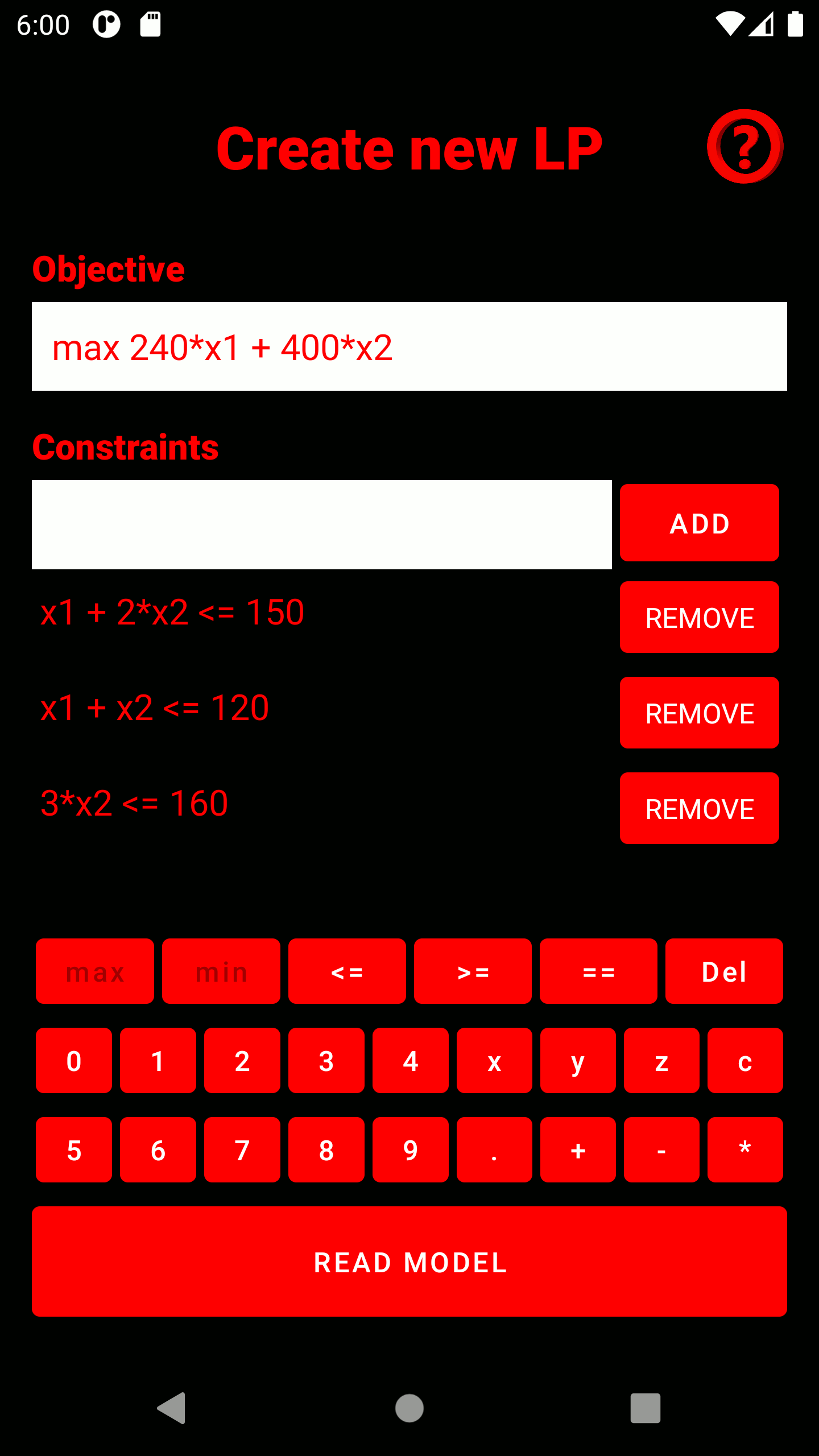
2. Type in your objective and all constraints. As soon as you click on the text field, a keyboard tailored to the input type appears. Constraints can be added to the model after input using the "ADD" button and appear below the input field. Incorrectly entered constraints can be deleted using the adjacent "REMOVE" button. The model is read in using the "READ" button.

3. The entire captured model is displayed here. It has already passed a read test and can be optimized. Below the model, the number of variables (without slack) and constraints is displayed. IMPORTANT: All variables are strictly positive, unless they have been explicitly bounded with a negative number (Example:
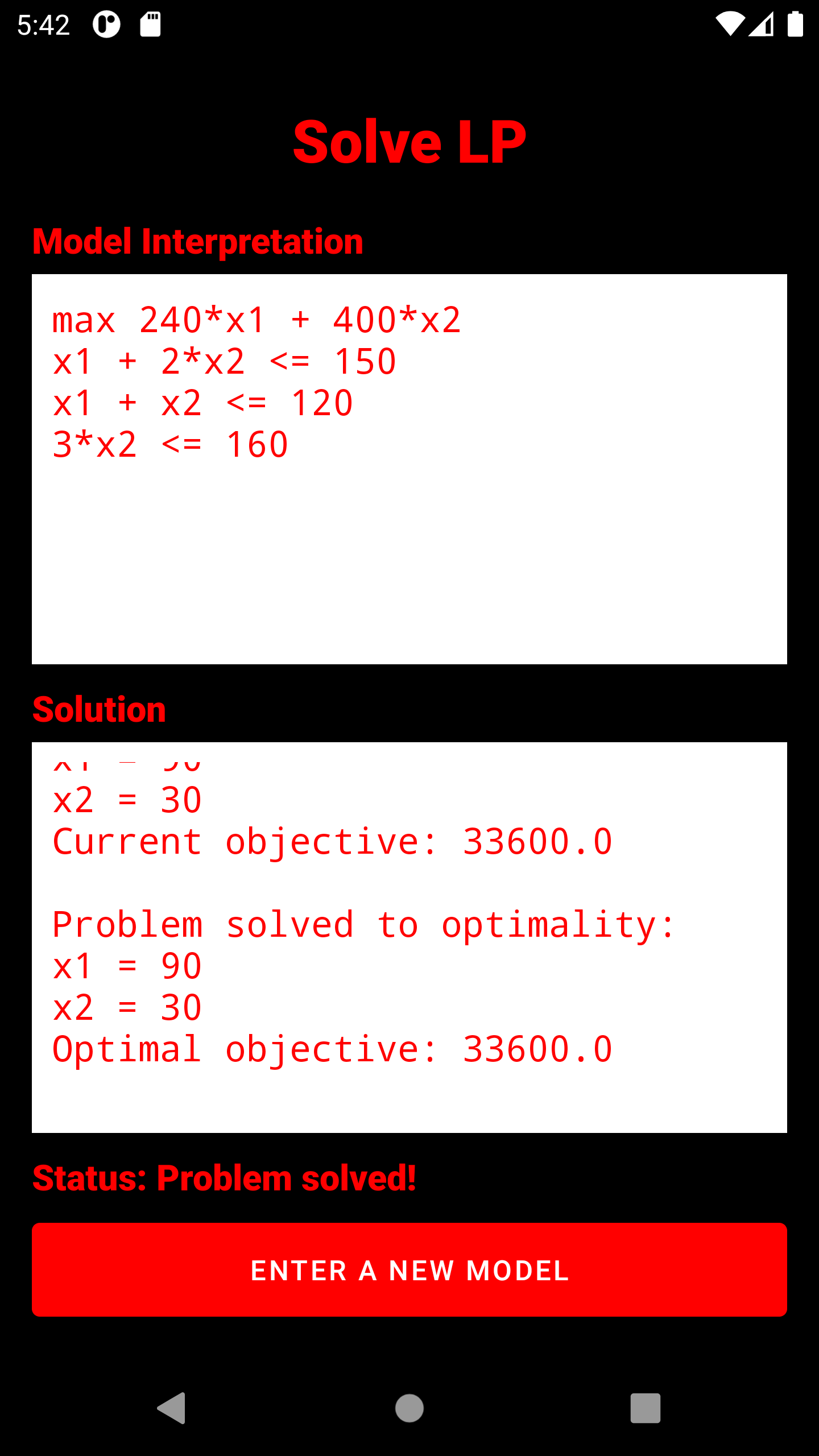
4. The simplex algrithm is triggered. Depending on the problem size, the display of the solution process varies. In any case, the optimal solution (if any) is displayed in the form of all variable assignments and the objective function value. The status display below the solution window indicates whether the problem is being processed, is infeasible, is unbounded, or is feasible.
Generate Random LP
The random generator was built to give an insight into the world of LP models. How can they be constructed and what notation underlies them when they are entered into the app? For this purpose only very small randomized models are generated, which always show a detailed model and solution output.

1. Select the middle Button "Generate random model"
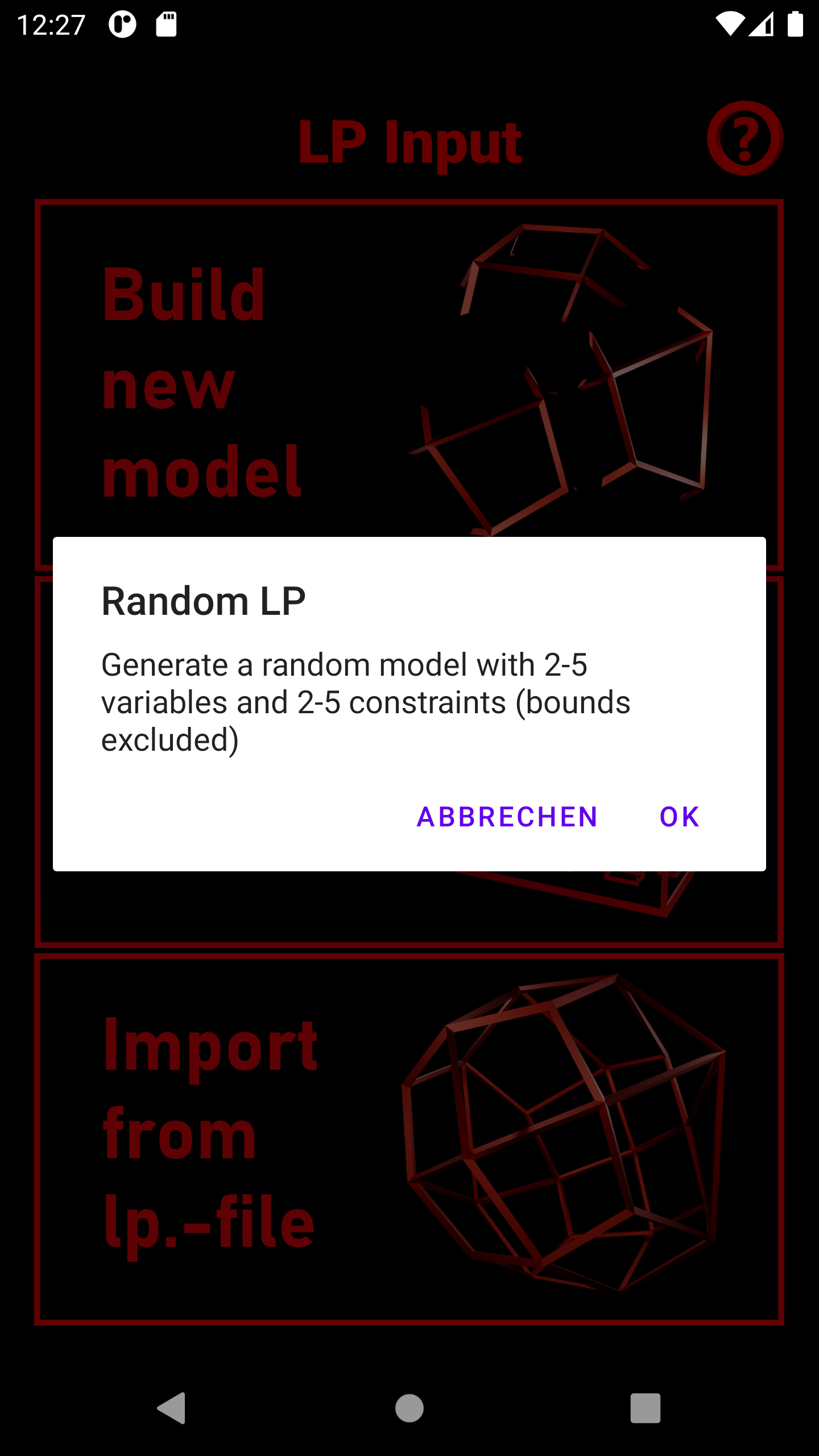
2. A pop-up-window will inform you, that a random model with 2-5 variables and constraints will be build. These random models are designed to be feasible. Generate the random model by pressing "OK". You have also the possibility to cancel the process.

3. The entire captured model is displayed here. It has already passed a read test and can be optimized. Below the model, the number of variables (without slack) and constraints is displayed. IMPORTANT: All variables are strictly positive, unless they have been explicitly bounded with a negative number (Example:
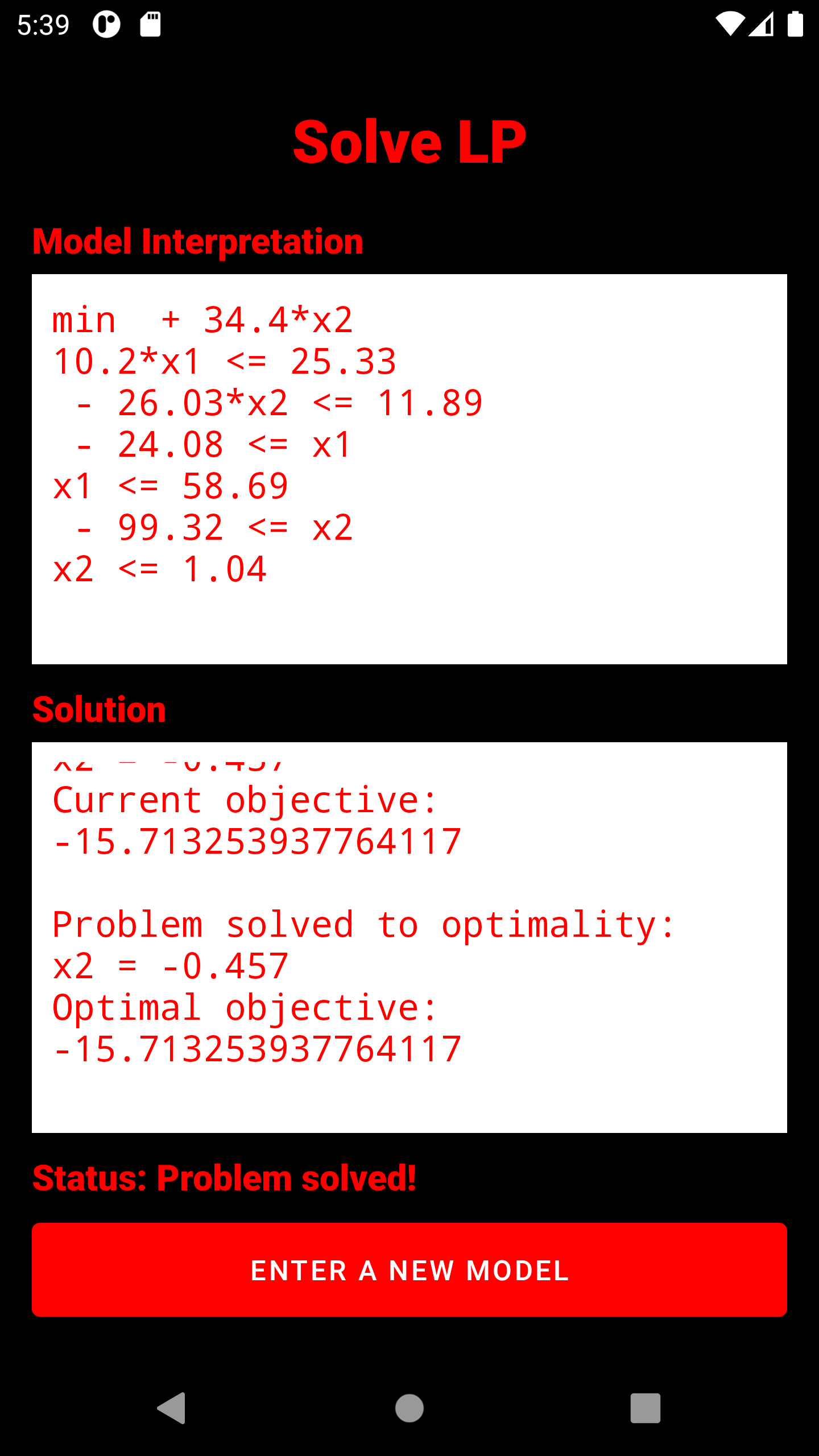
4. The simplex algrithm is triggered. The solution process will be displayed in detail. In any case, the optimal solution (if any) is displayed in the form of all variable assignments and the objective function value. The status display below the solution window indicates whether the problem is being processed, is infeasible, is unbounded, or is feasible.
Solve imported LP
To make it possible to solve larger models without having to re-enter them each time, classic .lp files can also be read. These can also be created independently on a computer. IMPORTANT: The implemented simplex algorithm serves didactic purposes and is not sufficiently performant for very large models. A maximum load of 10000 entries of the constraint matrix is recommended.

1. Select the lower Button "Import from .lp-file"
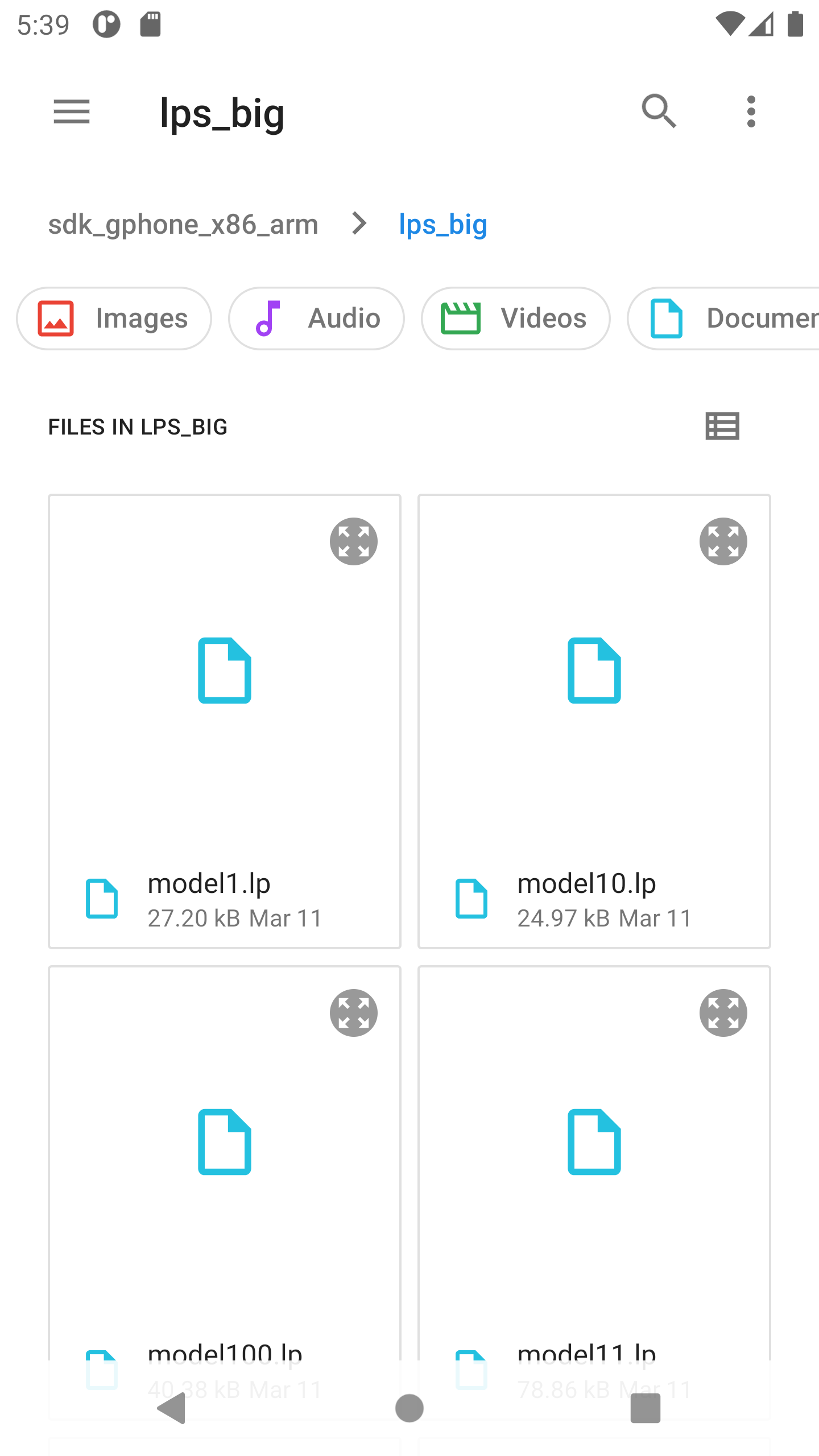
A window will open where you can select a file from your phone memory or external memory. Only files with the extension ".lp" are accepted. IMPORTANT: The LP file conventions apply. All coefficients must have been precalculated in this format and coefficients must be separated from variable by a space. In addition, the file needs an "END" tag.

3. The entire captured model is displayed here. It has already passed a read test and can be optimized. Below the model, the number of variables (without slack) and constraints is displayed. IMPORTANT: All variables are strictly positive, unless they have been explicitly bounded with a negative number (Example:
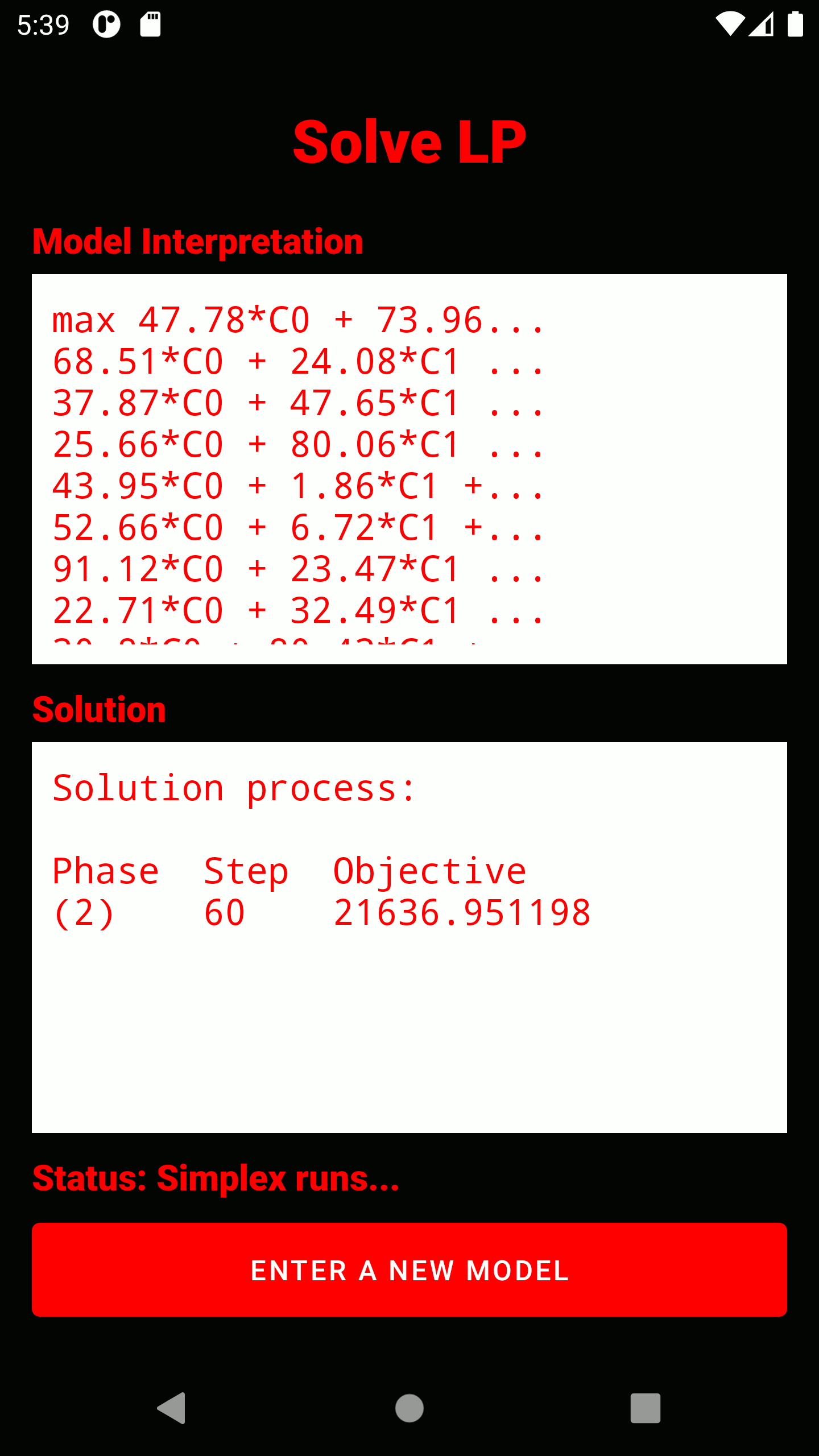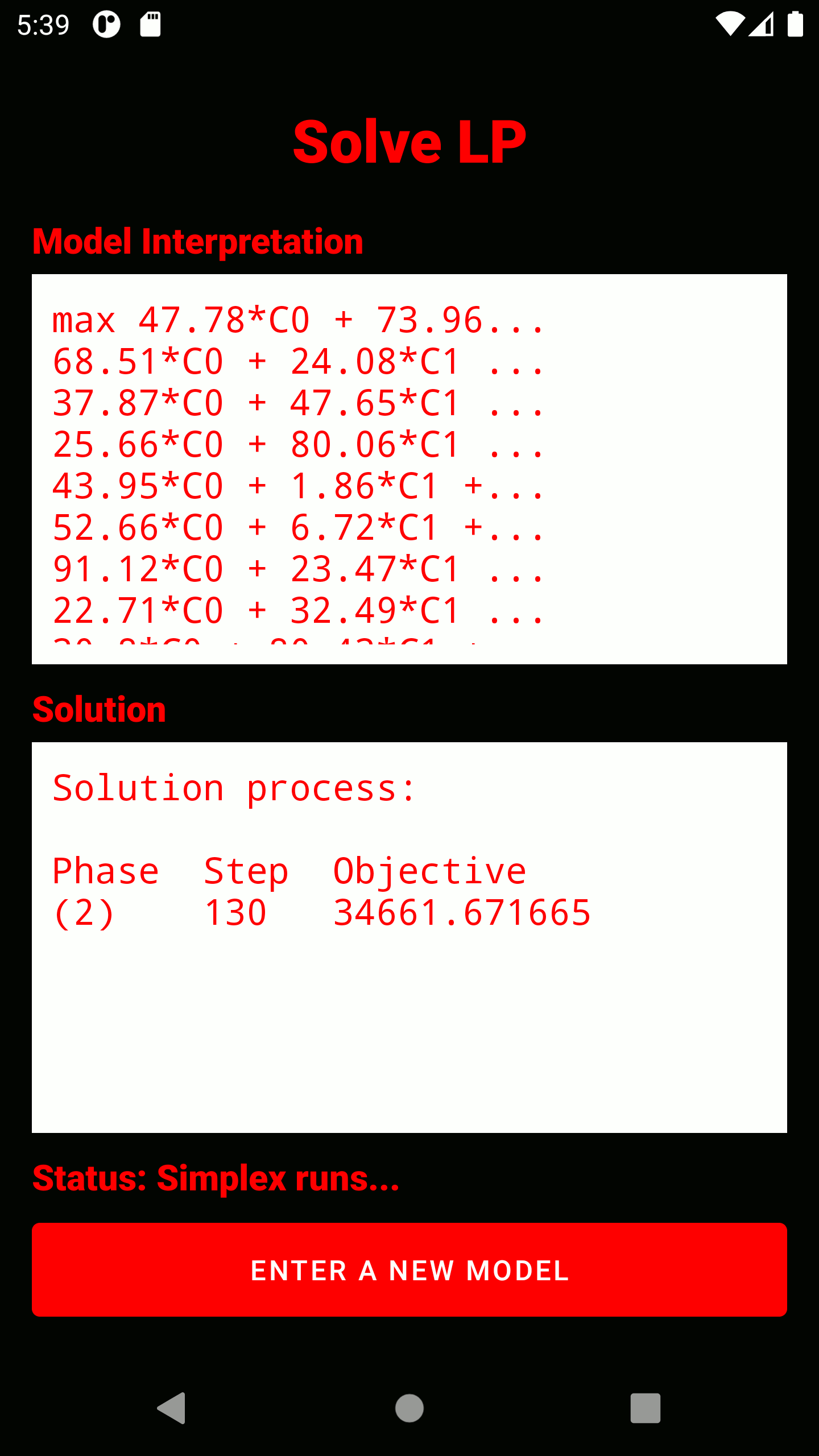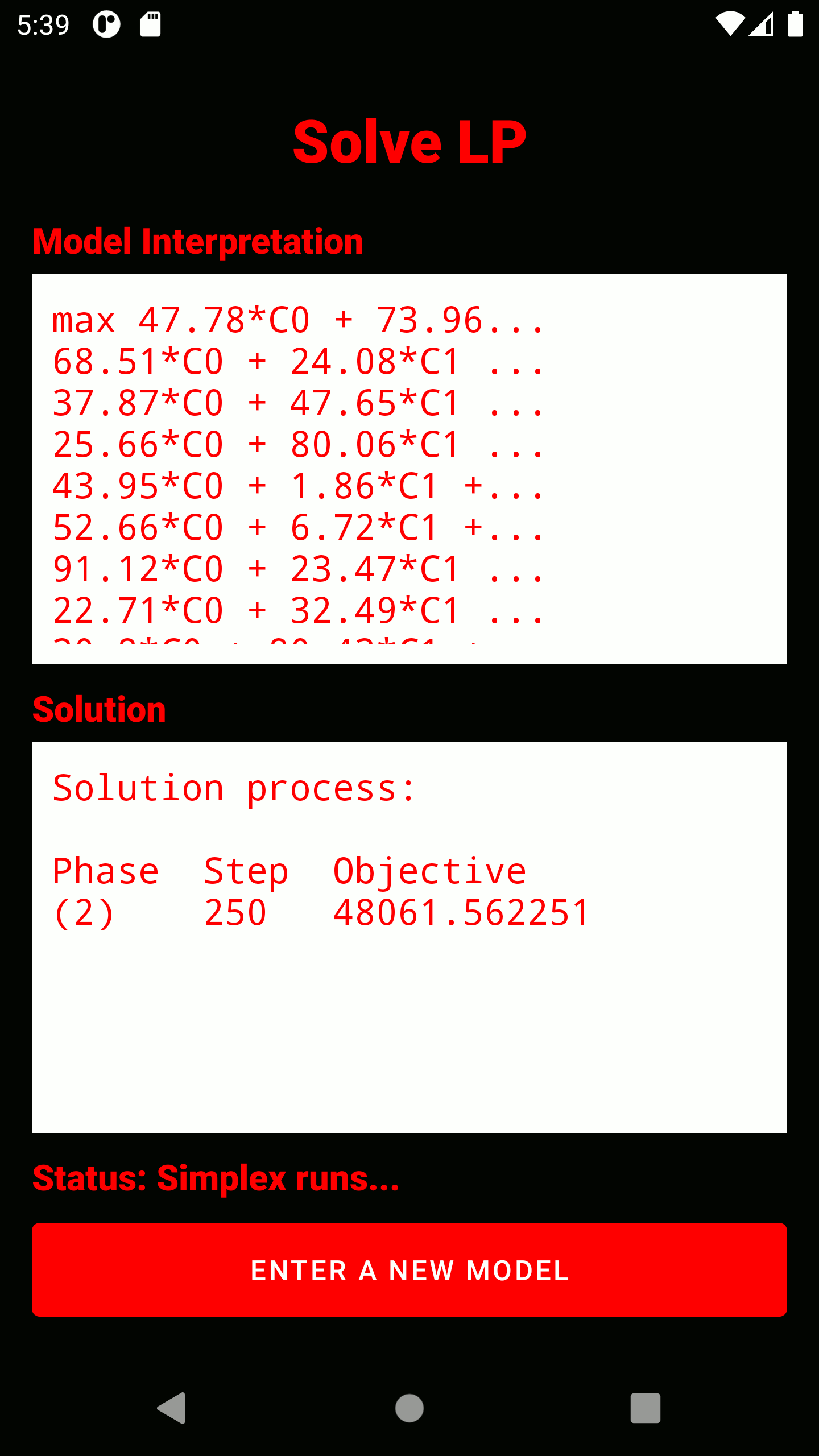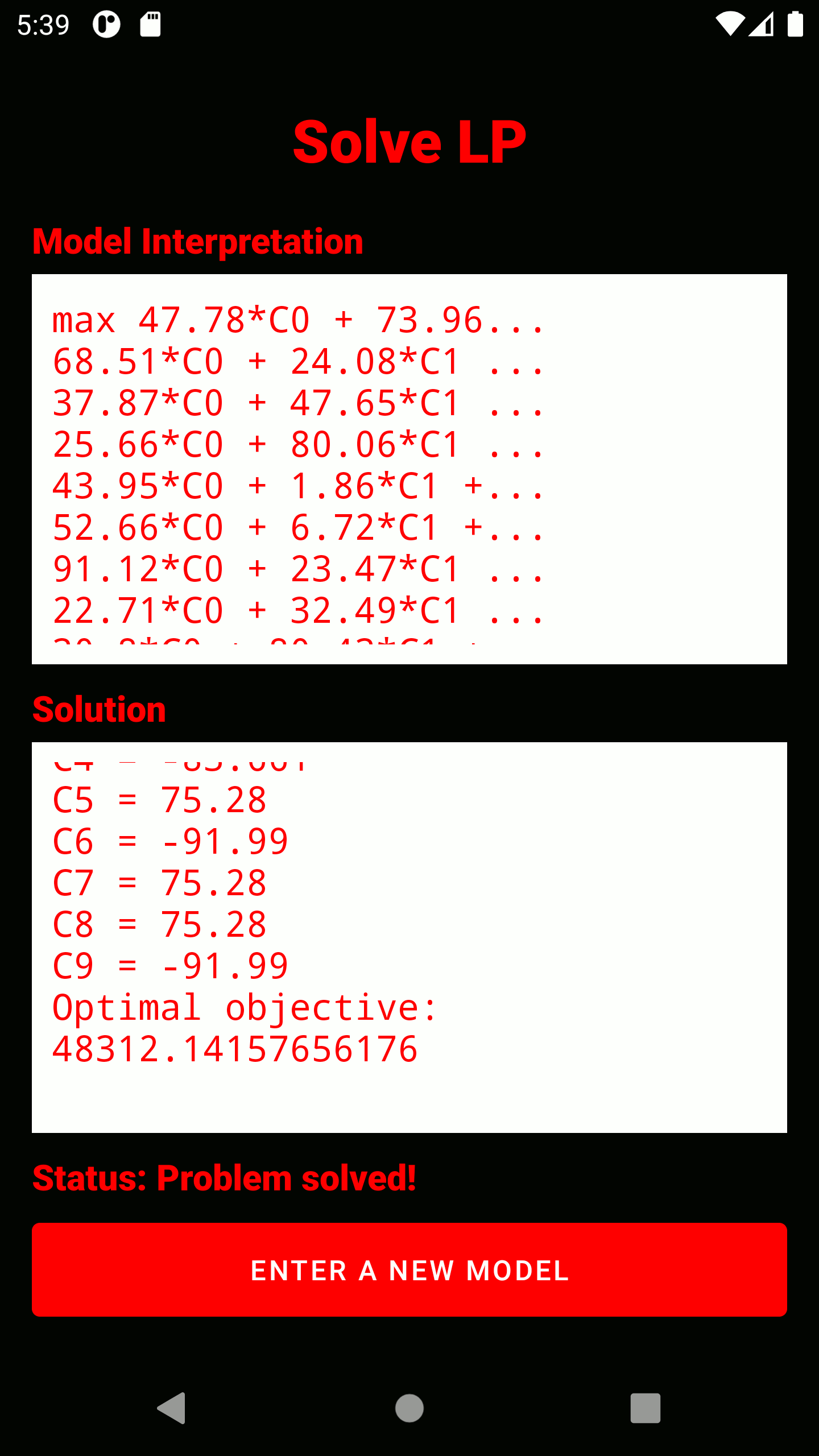
4. The simplex algrithm is triggered. The solution process will be displayed reduced. In any case, the optimal solution (if any) is displayed in the form of all variable assignments and the objective function value. The status display below the solution window indicates whether the problem is being processed, is infeasible, is unbounded, or is feasible.
Bugs
If you find any errors in the app, please do not hesitate to contact me via lukas.dev.apps@gmail.com.
